Our research interests include causal inference, graphical models, generalised Bayesian inference, statistical analysis of complex stochastic systems, and methodologies and theoretical foundations for large-scale learning problems.
You can also see our Publications.
Bayesian nonparametrics and high-dimensional models
This area concerns the development of Bayesian methods for high dimensional of infinite dimensional methods, together with the study of their theoretical properties. The increase of complexity of the data sets and the models often imply that approximate computational approaches are used and the study of their theoretical properties is also a subject of ongoing research."
Causal inference
Causal inference involves discovery (determining the direction of causation between different variables) and inference (quantifying the strength of causality). Researchers in the group work on both problems.
Statistical analysis of complex stochastic systems
Real world data often challenge us with complex structural features. In this research we develop models for data using combinatorial structures such as trees, directed graphs and partial orders. Stochastic process models for time series of these objects are sometimes needed. Building and fitting such models leads to new statistical and computational methods
Generalised Bayesian inference
When we apply Bayes Methods to data model misspecification is often an issue. Researchers sometimes treat this problem by modifying the inference, rather than the model. This must be done in a principled way and is the subject of ongoing research.
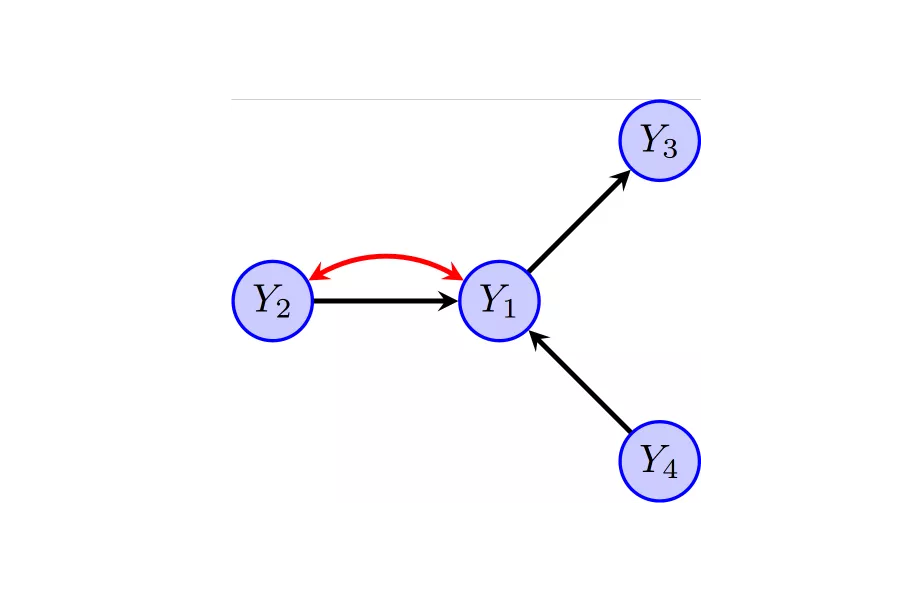
Graphical models
Graphs can be used to represent the dependence structure of random variables, where (typically) the absence of an edge implies a conditional independence. Our researchers are particularly interested in directed and mixed graphical models, which can account for unobserved confounding in causal systems.
Statistical learning and reinforcement learning theory
This area of research concerns the mathematical formalisation of a variety of learning frameworks in offline/online settings, with the aim to develop methodologies that are provably statistically and computationally efficient/optimal.

