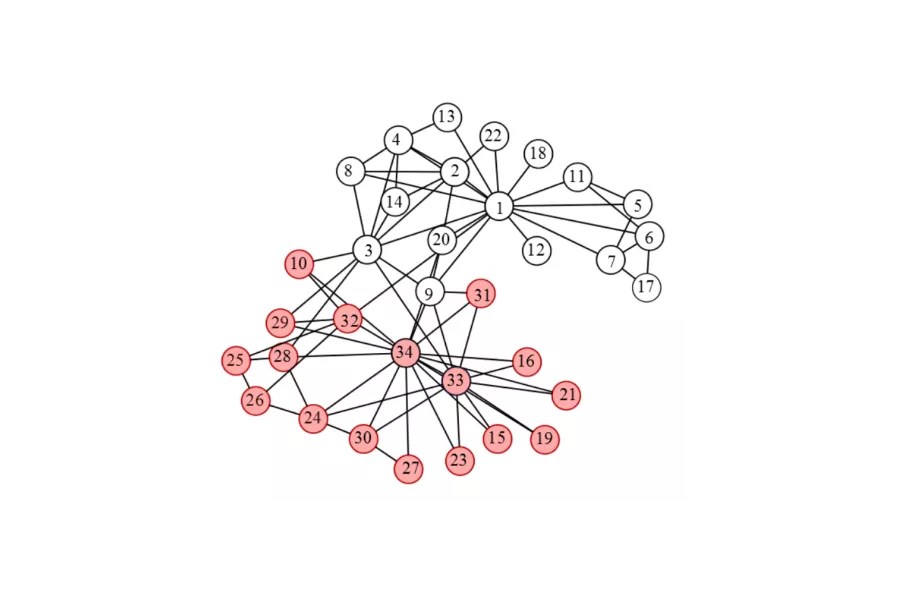
Networks are often used as representations of complex data sets. In order to understand such representations, random network models are a useful tool. Randomness in networks is typically included by fixing a vertex set and modelling the collection of edge indicator variables via a random model. Interesting probabilistic questions arise from such models; even the typical behaviour of the number of subgraphs of certain types can be challenging.

Another problem area is that of comparing networks in a meaningful way; answers to this question could be used to try to tease out evolutionary information from protein interaction networks. A third area of research is synthetic data generation: given a network, how can we generate synthetic networks which capture essentials of the given network without being identical to it, and can we give theoretical guarantees for such network generators?

Limiting behaviours under different regimes are also a very active area of research.

Much of Gesine Reinert's work is focussed on network analysis.

Random trees, and branching structures more generally, occupy a central place in modern probability.  They encompass a broad family of different models, such as branching particle systems, processes of coalescence and fragmentation, as well as classical branching processes, random combinatorial trees, and the scaling limits of these objects.  Such models play a key role in studying situations as diverse as population genetics, cancer growth, epidemiology, nuclear reactions and the analysis of algorithms, to give just a few examples. Recently, stochastic models of branching have also proven themselves to be surprisingly useful in a priori unrelated fields of mathematics such as number theory and partial differential equations.

Branching structures lie at the heart of the work of several of our researchers including Julien Berestycki, Alison Etheridge, Christina Goldschmidt, James Martin and Matthias Winkel.

Originating in a ground-breaking paper from 1972 by Charles Stein, Stein’s method has become a tool of choice for assessing distances between probability distributions. It is particularly well suited to provide bounds which depend explicitly on the number of observations as well as parameters of the underlying distributions, and can be powerful even when the underlying distributions  relate to dependent random elements. In the last decade, tests and procedures based on key quantities in Stein’s method have been developed in machine learning to assess tasks such as goodness of fit tests. In the area of networks, an example is given by AgraSSt (Xu and Reinert, NeurIPS 2022) which assesses the quality of a synthetic graph generator. Stein's Method plays a large role in the work of Gesine Reinert.