A variant on this idea which has been suggested many times is to add
`noise' to the training set, randomly perturbing either the feature
vectors 
or the classes (or both). Further along this
line, we could model the joint distribution of 
and create new training sets from this distribution. Bagging can be
seen as the rather extreme form of this procedure in which the model
is the empirical distribution. (Krogh & Vedelsby,1995, use
cross-validation rather than re-sampling, and consider designing
training sets weighted towards areas where the existing classifiers
are prone to disagree.)
Boosting [Schapire,1990; Freund,1990; Drucker et al.,1993; Drucker et al.,1994; Freund,1995; Freund & Schapire,1995; Freund & Schapire,1996a] is altogether more ambitious. The idea is to design a series of training sets and use a combination of classifiers trained on these sets. (Majority voting and linear combinations have both been used.) The training sets are chosen sequentially, with the weights for each example being modified based on the success of the classifier trained on the previous set. (The weight of the examples which were classified incorrectly is increased relative to those which were classified correctly.) For classifiers that do not accept weights on the examples, resampling with probabilities proportional to the weights can be used.
There have been a number of practical tests of boosting, including Drucker (1996);Drucker & Cortes (1996);Freund & Schapire (1996b);Breiman (1996c) and Quinlan (1996a). Each of Freund & Schapire, Breiman and Quinlan compare bagging and boosting for classification trees (although only Quinlan used weighting rather than weighted re-sampling for boosting), and all find that boosting usually out-performs bagging but can fail so badly as to make the boosted classifier worse that the original.
The original motivation for boosting was to produce a combined classifier that could fit the training set perfectly by concentrating on the regions of the feature space which the current classifier found hard. As both Breiman and Quinlan point out, this is a very different aim from producing a classifier with good generalization in problems with overlapping classes, a problem which requires boosting beyond the point needed to fit the training set perfectly. It seems likely that greater study of boosting will lead to algorithms designed to boost generalization error.
Cesa-Bianchi et al. (1993);Cesa-Bianchi et al. (1996) consider how to learn how to do as well as the best of a class of classifiers over a sequence of examples, and derive bounds for the excess errors made whilst learning which is best. This is a different goal from the usual one in combining classifiers, which is to do better than even the best classifier by exploiting the strengths of all. The algorithm used is boosting-like, maintaining weights for each expert rather than each example.
In (2.50) the factor 1/8 in the exponent can be removed. Parrondo & Van der Broeck (1993) give
and Vapnik(1995, pp. 66, 85) quotes the constant 4 as in (2.50), although proofs are deferred to the forthcoming Vapnik (1996).
The improvements of Parrondo & Van der Broeck rely on
- [(i)]
- Replacing (2.55) by
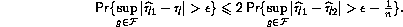
This follows from the binomial inequality
for each choice of sign, and so, conditionally on the first sample
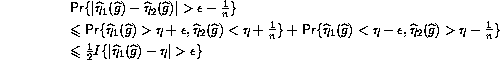
Inequality (1) says that for a binomial distribution the median lies within one of the mean; it seems well-known to combinatorists, none of whom was able to give me a reference.
- replacing the use of Hoeffding's inequality at the top of page 87
by an inequality of Vapnik (1982):
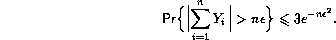
The bound for proposition 2.5 may be improved to
by the same ideas. (The statement in
Parrondo & Van der Broeck,1993, does not follow from their
proof and appears to be wrong.)
misclassifications is NP-hard. (For k = 0 it is
reducible to a linear programming program as shown on this page, so
solvable in polynomial time.)
by unity at each step, large weights
entail slow convergence.
, and 
. More recently Håstad found an
example which needs integer weights at least as large as 
. These results are reviewed and proved by
mistakes before finding a linearly
separating solution, a bound reduced to 
by
mistakes
are necessary on some problems with p binary inputs.).
whilst insisting that 
. Finding this hyperplane is a
quadratic programming problem, and the usual Kuhn-Tucker optimality
conditions show that there will be a subset of examples 
(known
as support vectors) for which 
and that the
optimal 
was also proposed by Werbos (1987).
and 
results fails to make clear what is allowed to vary; these results apply
to networks where both the number of input units and the number of
hidden units are allowed to increase. In that case Sakurai (1993) has
. 
if the inputs are restricted to 
.
)
where 
is proportional to the average distance to the, say,
first 5 neighbours, and 
is weighted by weights for each
feature. (Thus a quadratic metric with diagonal A is used.) Both the
constant of proportionality and the metric are chosen by
(leave-one-out) cross-validation. Like that of Fukunaga & Flick (1984)
this is a global method, but Lowe mentions that the feature weights
could be chosen locally, as was done by Atkeson (1991) in a control
problem. The restriction to a diagonal metric places the pre-processing
of the features at a premium.
distance with a diagonal weighting matrix) by recursive
partitioning on this relevance measure. The proposal of
Hastie & Tibshirani is much simpler; they use Euclidean
distance on the linear discriminants for points within a small
neighbourhood (defined by this metric and so chosen recursively).
, whereas for a nominal
attribute any split of the values into two groups is allowed,
and this can result in splitting a discretized continuous attribute
into a series of intervals and their complement. Indeed,
Holte (1993) and Auer et al. (1995) have shown that very shallow
trees (one level or two levels respectively) can be rather effective
on many common problems if splits of this sort are allowed.
.)
is defined on page 178.
where M
is the number of sigmoidal units