RecMin software

by S.R.Myers

Under certain assumptions the pattern of diversity at a collection of linked sites provides information allowing us to detect historic recombination events. The program RecMin.c calculates a lower bound on the number of recombination events required to construct any history of a sample, under the assumption that each segregating site has mutated only once since the most recent common ancestor of the sample. Such a lower bound is appropriate, since many historical recombinations are typically undetectable. It gives a measure of what extent the sample history differs from a simple tree structure, and can show if there is regional clustering of the detectable recombinations.

Given an input set of sequence data, the program outputs two minimum numbers of recombination events; firstly, the statistic R_m of Hudson and Kaplan (1985), that employs the four-gamete test; and secondly, a new bound, R_h or R_s (described in Myers and Griffiths, 2003), depending on the input settings. These correspond to a minimal number of recombination events over the whole region; for any dataset, the new lower bound will be at least equal to R_m and can be considerably larger. R_m can be interpreted as a minimal number of different positions at which recombination occurred (Wiuf, 2003), whilst the new bounds R_h and R_s give a minimum to the number of events that have happened (more than one event might potentially occur at a position).

The program can be used on datasets of any size with diallelic loci, in binary format. For details on the format accepted and an example dataset, see the file testdata.txt . Currently only haplotype data is processed. The code has recently been modified to allow for the possibility of some data being missing.

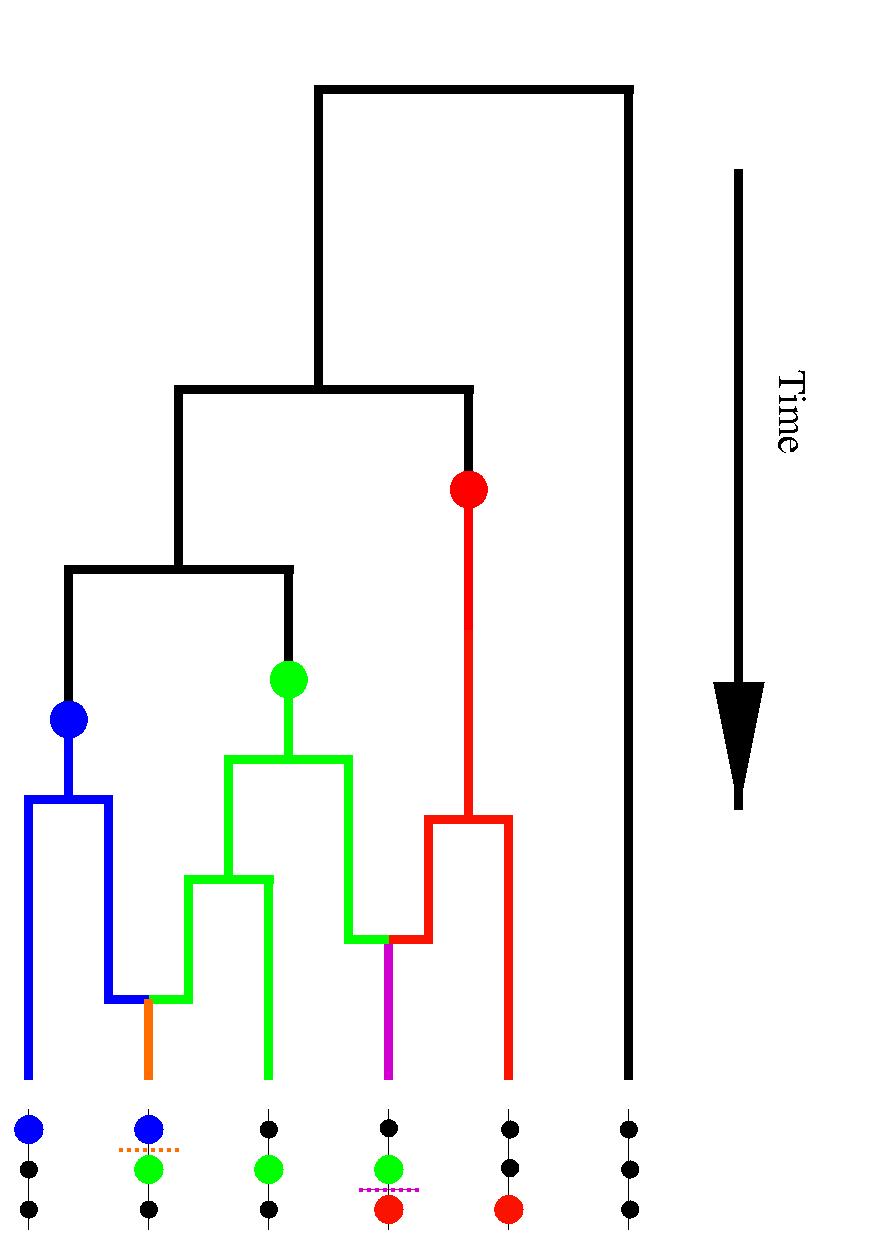
The properties of the various bounds under coalescent simulations are explored further in Myers and Griffiths (2003). The respective bounds R_h and R_s employ two different algorithms to obtain local lower bounds for sub-regions of the data (analogous to the four-gamete test results used to give R_m), which are then combined in an optimal way to give the overall bound for a region. R_h employs the haplotype bound, which uses the number of different observed types to bound below how many of these are recombinants (this idea is illustrated in the figure shown above, where at least two of the types illustrated at the bottom must be recombinants). R_s uses an approximation of a recombination history of the sample to give better, but more computationally intensive, lower bounds in the case where none of the data is missing.

The output is placed in a file, and consists of either just the bounds, or optionally a more detailed matrix showing the number of recombinations required between every pair of sites. This matrix can be plotted to give a visual impression of where within a region the detected recombination events are clustered; this may allow regions of interest (e.g. potential recombination hotspots) to be observed. R code to produce plots of such matrices, similar to those shown in Myers and Griffiths (2003), is available on request by emailing myers@stats.ox.ac.uk. The program can handle multiple datasets in a single file.

The directory RecMin contains versions of RecMin.exe suitable for use on Windows/DOS, and also Unix machines. The entire directory is available as a gzipped tar file here. The original C source code may be found in the file RecMin.c, which can be compiled on other operating systems. There is also a file Readme.txt that gives the necessary details for compilation, and instructions on running the program/options accepted.

If you intend using RecMin or are interested in the approaches considered in Myers and Griffiths (2003), please email the authors at myers@stats.ox.ac.uk . Please also email if you have any problems with data conversion or running the code, with details of any bugs you may find, or with any suggestions for possible improvements to the program.

References:

Myers, S. and Griffiths, R. C., Genetics 163(1):375-394, Jan. 2003

Hudson, R. R. and Kaplan, N., Genetics 111:147-164, Sep. 1985

Wiuf, C., Theor. Pop. Biol. 62(4):357-363, Dec. 2002