Department of Statistics
Oxford University
Oxford OX1 3TG, UK
clifford@stats.ox.ac.uk
22/12/94

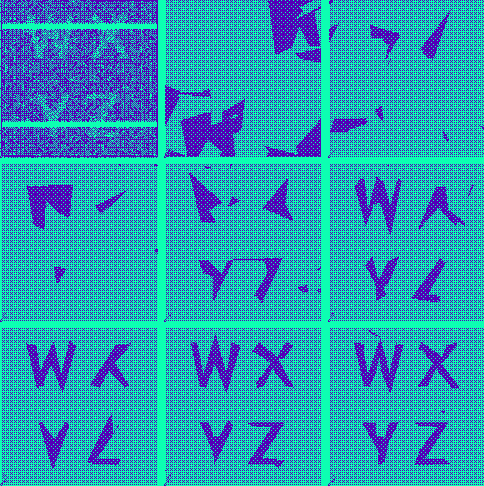
We show how a stochastic model of polygonal objects can provide a Bayesian framework for the interpretation of colouring data in the plane. We describe a particular model and give a Markov Chain Monte Carlo (MCMC) algorithm for simulating the posterior distribution of the polygonal pattern.
Two important observations arise from our implementation of the algorithm. First, it is computationally feasible to use MCMC to simulate the posterior distribution of a polygonal process for moderately large problems ({\it{ie}}, 10000 data points, w ith polygonal patterns involving around 120 edges). Our implementation, which we would describe as careful, but unsophisticated, produces satisfactory approximations to the mode of the posterior in about 5 minutes on a SUN Sparc 2. Independent samples from the posterior take a few seconds to generate.
The second observation is that the Arak process, a particular type of polygonal process, makes a wonderful debugging tool for testing shape simulation software. This is no mundane observation. Given the usually very complicated nature of such software it is essential to demonstrate that samples genuinely do come from whichever shape distribution is proposed. The Arak process has the advantage that many of its properties can be expressed in precise analytic terms. Computer programmes designed to sample mosaics formed from polygonal shapes can thereby be tested on this process by comparing computer output with exact theoretical expectations.