Matlab/Octave demo - Two-sample Bayesian nonparametric hypothesis testing
This Matlab/Octave script provides a demo on the Bayesian nonparametric Polya tree test described in (Holmes et al., 2014), and reproduces most of the figures in the paper.
C.C. Holmes, F. Caron, J.E. Griffin, D.A. Stephens. Bayesian Analysis, to appear, 2014. Download paper.
Author: F. Caron, University of Oxford
Tested on Matlab 2014a with Statistics toolbox and on Octave 3.6.4.
Contents
- Download and Installation
- Simple demos of the subjective and conditional tests
- Power curves and posterior probabilities for the subjective test
- Distribution of log-ratio as a function of the sample size, under the null and various alternatives
- Power curves and posterior probabilities for the conditional test
- Distribution of the log-contributions at different levels of the tree
- Sensibility to the parameter c
Download and Installation
- Download the zip file containing the .m files
- Unzip the archive in some folder
- Add the folder to the Matlab/Octave path
mfiles_path = '.\'; % Indicate the path to the folder addpath(mfiles_path); % Add to the Matlab/Octave path
Check if running Octave or Matlab
close all clear all set(0,'DefaultAxesFontsize',16) set(0,'DefaultAxesColorOrder',[0 0 0],... 'DefaultAxesLineStyleOrder','-|--|-.|:') set(0,'DefaultLineLinewidth',3) isoctave = (exist('OCTAVE_VERSION')~=0); % Checks if octave running if ~isoctave rng('default'); else rand ('state', 'reset'); end
Contents
if ~isoctave help Polyatreetest end
Contents of Polyatreetest: PTtest - performs a two-sample test based on a Polya tree prior demoPolyatreetest - Matlab/Octave demo - Two-sample Bayesian nonparametric hypothesis testing powercurve - computes power curves for the Polya tree, KS and Wilcoxon tests testfunc - runs the functions PTtest and powercurve with different parameters
Simple demos of the subjective and conditional tests
n = 50; y1 = randn(n, 1); y2 = .5 + randn(n, 1); % Subjective Polya tree test with empirical estimation of c [h, post, stats] = PTtest(y1, y2, 'estimate_c', true); fprintf('Subjective test: P(H0|y1,y2)=%.2f\n', post) % Conditional Polya tree test with empirical estimation of c [h, post, stats] = PTtest(y1, y2, 'estimate_c', true, 'partition', 'empirical'); fprintf('Conditional test: P(H0|y1,y2)=%.2f\n', post)
Subjective test: P(H0|y1,y2)=0.50 Conditional test: P(H0|y1,y2)=0.50
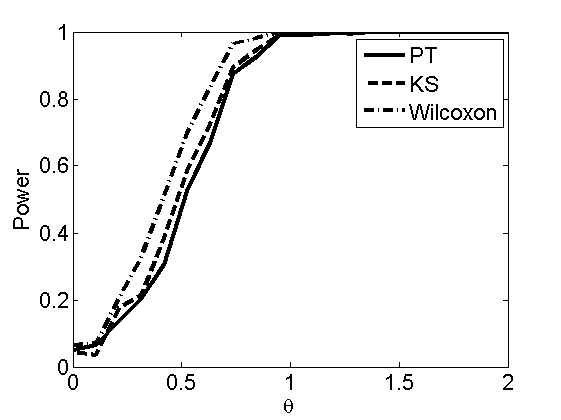
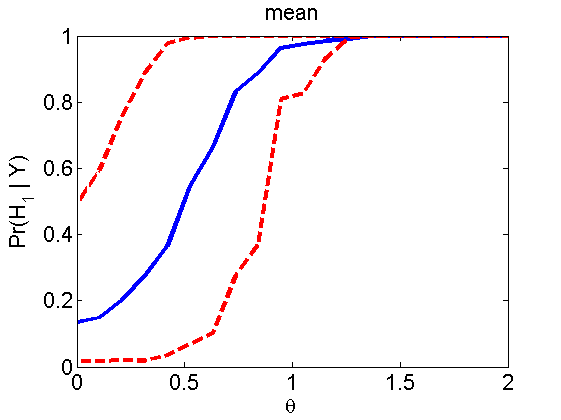
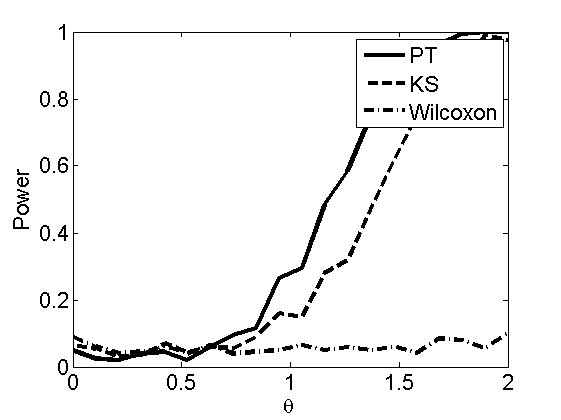
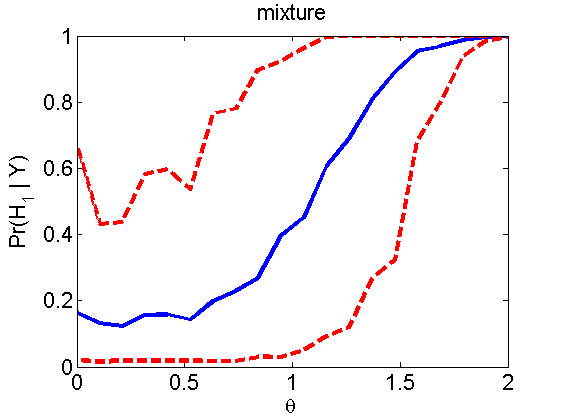
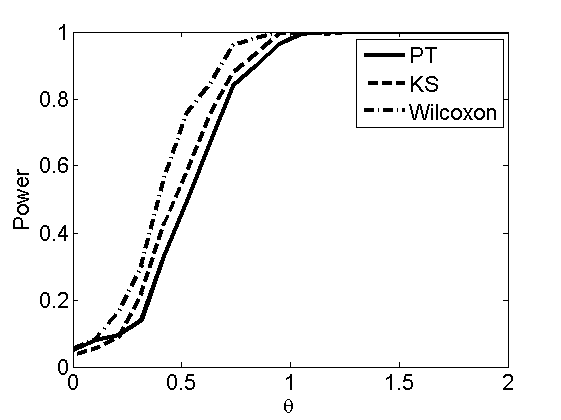
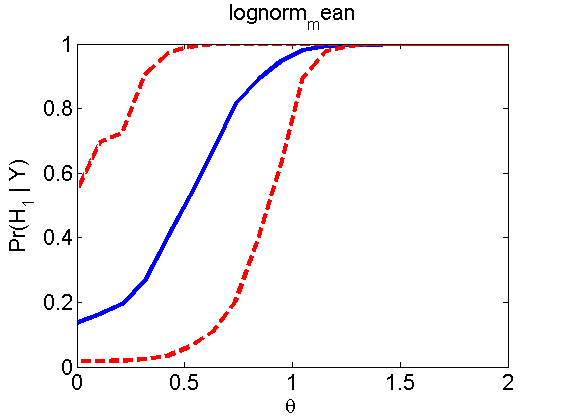
Power curves and posterior probabilities for the subjective test
(Figures 2 in the paper)
nsamples = 200; % Number of samples - Note: 1000 were used to create the figures in the paper n = 50; types = {'mean', 'var', 'mixture', 'tail', 'lognorm_mean', 'lognorm_var'}; for k=1:length(types) type = types{k}; [theta_trial, polyatree, kolmo_smir, wilcoxon, LOR, h, h2] = powercurve(n, type, ... 'nsamples', nsamples, 'doplot', true); figure(h) title(type); figure(h2) title(type); end
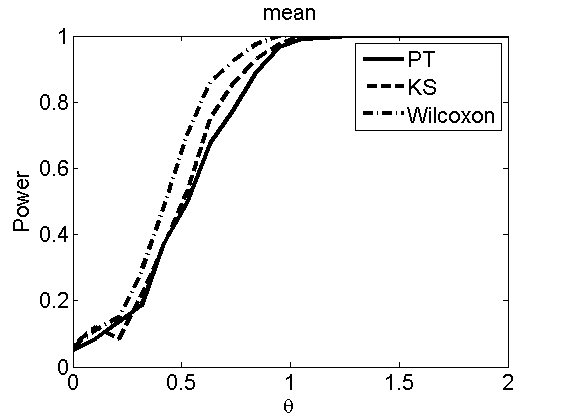
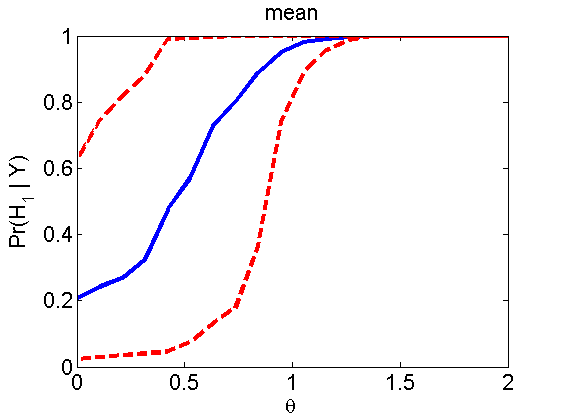
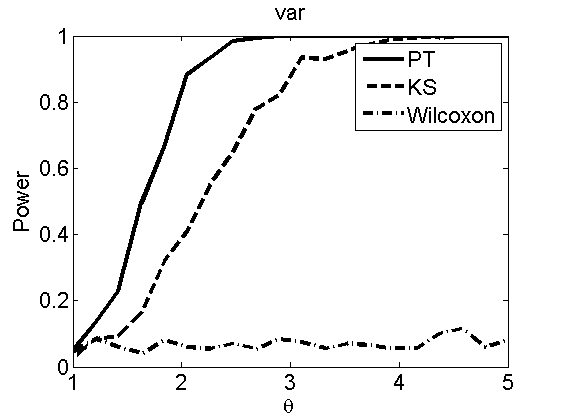
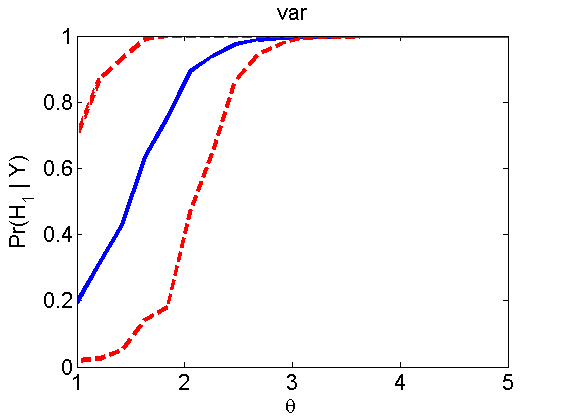
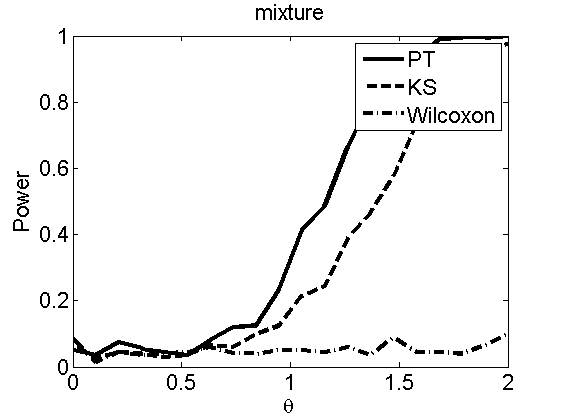
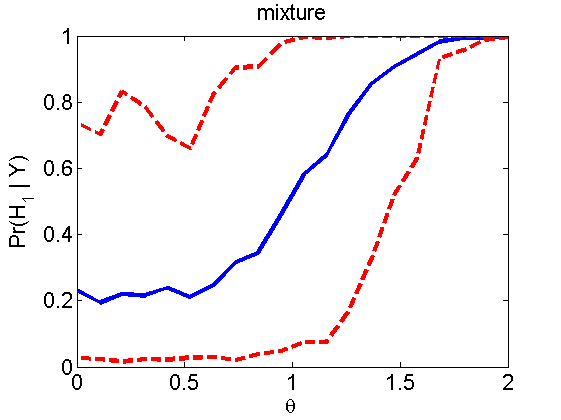
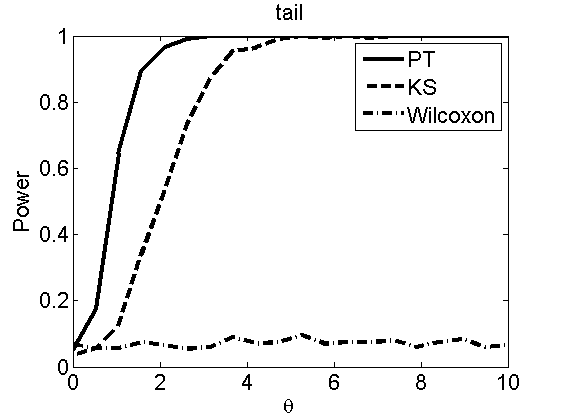
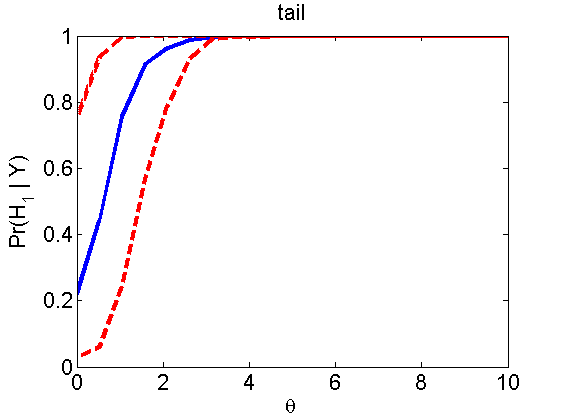
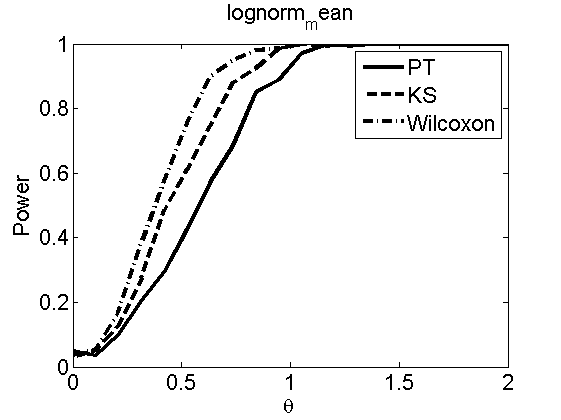
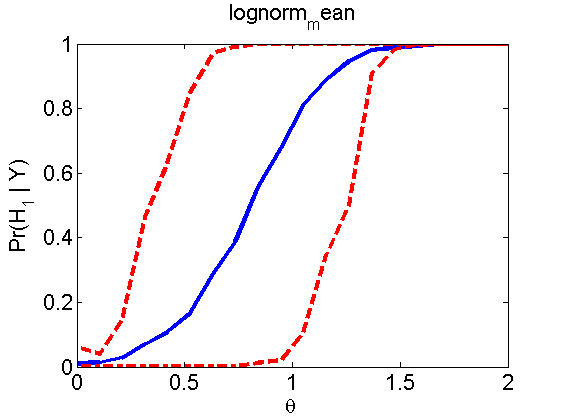
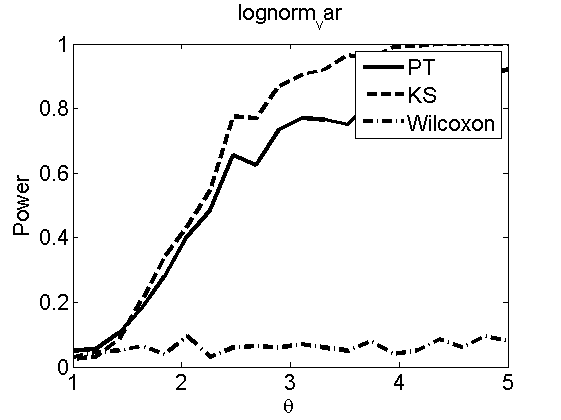
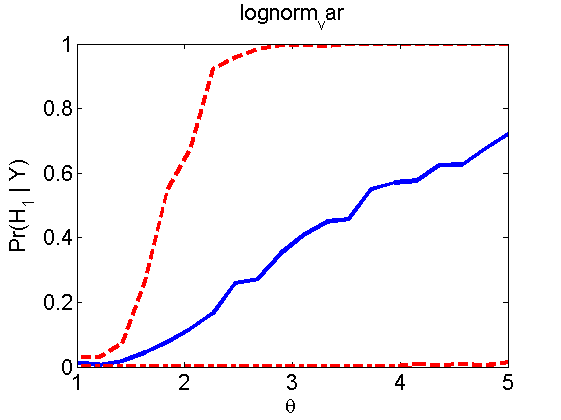
Distribution of log-ratio as a function of the sample size, under the null and various alternatives
(Figure 4 in the paper)
n_all = [10, 50, 100];%[10, 50, 100, 150, 200]; LOR = zeros(length(n_all), nsamples); for i=1:length(n_all) n = n_all(i); for j=1:nsamples % Null y1 = randn(n,1); y2=randn(n,1); [h, post, stats] = PTtest(y1, y2); LOR(i,j,1) = stats.LOR; % Alternative: Mean y1 = randn(n,1); y2 = 1 + randn(n,1); [h, post, stats] = PTtest(y1, y2); LOR(i,j,2) = stats.LOR; % Alternative: Var y1 = randn(n,1); y2 = 3 * randn(n,1); [h, post, stats] = PTtest(y1, y2); LOR(i,j,3) = stats.LOR; % Alternative: Tails y1 = randn(n,1); y2 = trnd(1/5,n,1); [h, post, stats] = PTtest(y1, y2); LOR(i,j,4) = stats.LOR; end end titles = {'Null', 'Alternative: Mean', 'Alternative: Variance', 'Alternative: Tails'}; for k=1:4 figure('name', 'Figure 4'); mean_LOR = mean(LOR(:,:,k), 2)'; low_LOR = quantile(LOR(:,:,k)', .05); up_LOR = quantile(LOR(:,:,k)', .95); plot(n_all, LOR(:,:,k)) errorbar(n_all, mean_LOR, up_LOR-mean_LOR, mean_LOR-low_LOR) xlabel('Sample size n', 'fontsize', 16) ylabel('Log Bayes Factor', 'fontsize', 16) set(gca, 'fontsize', 12) title(titles{k}) end
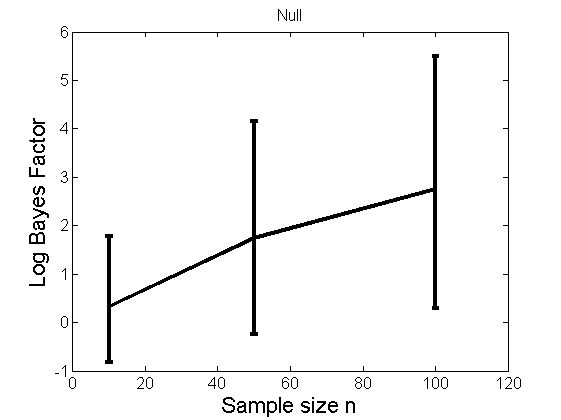
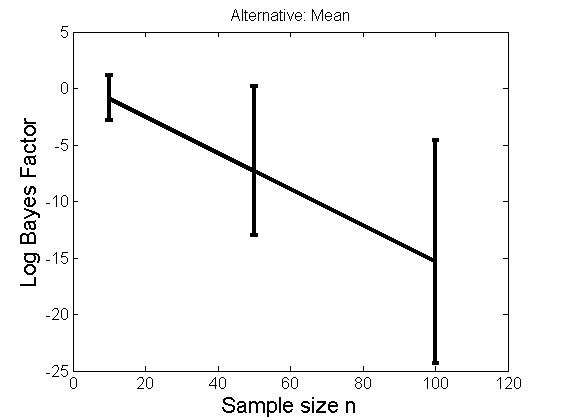
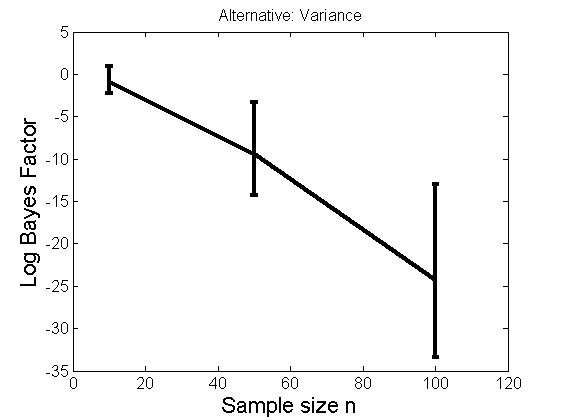
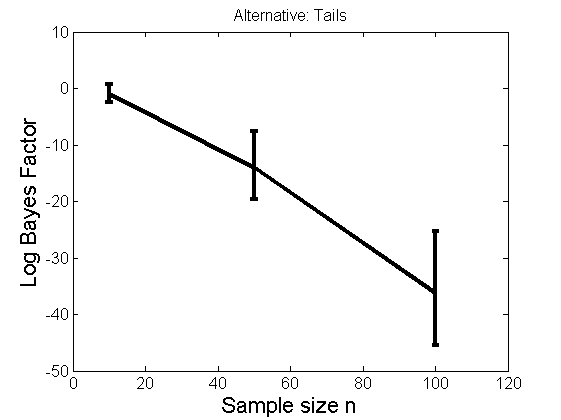
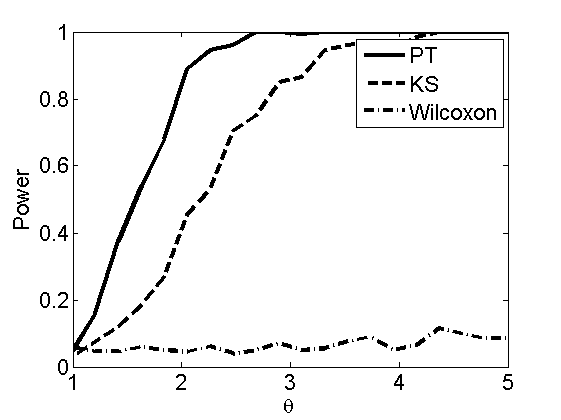
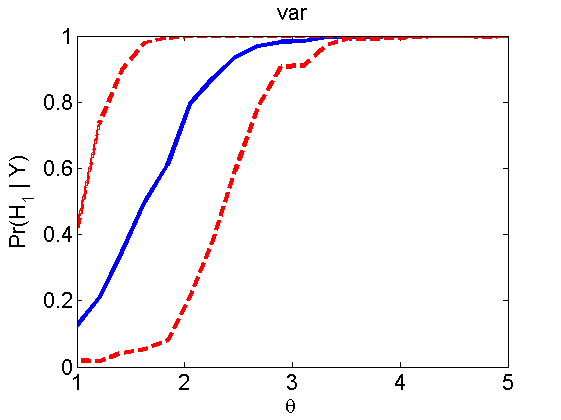
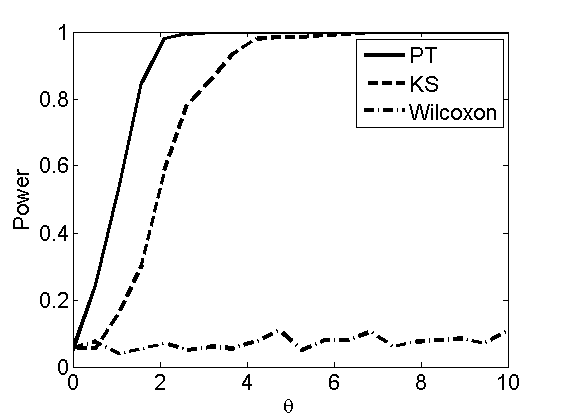
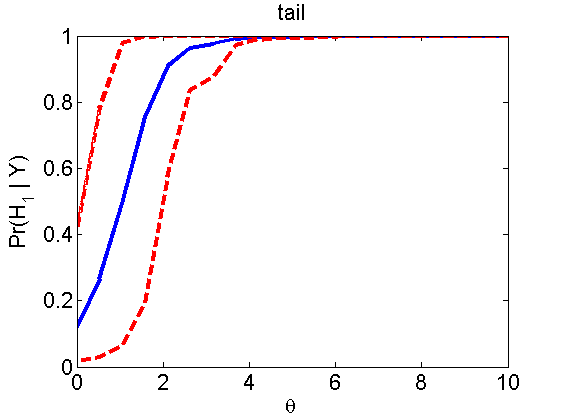
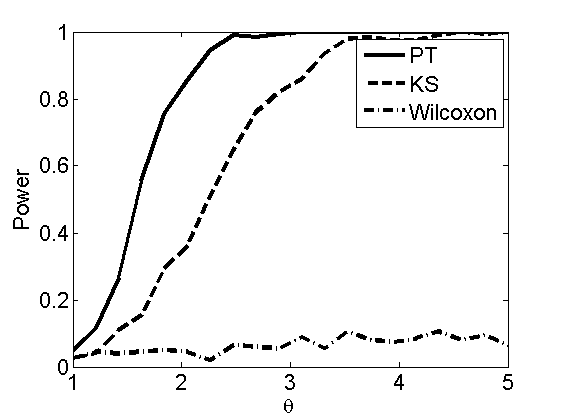
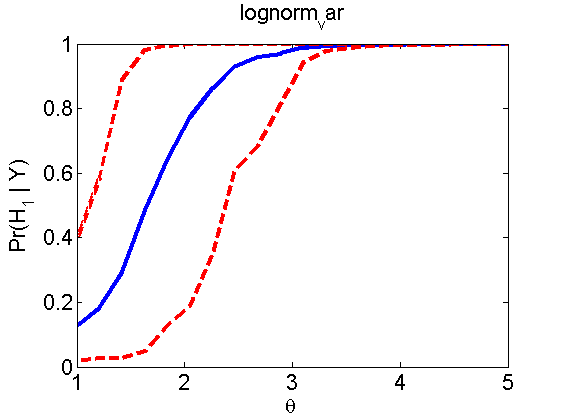
Power curves and posterior probabilities for the conditional test
(Figure 5 in the paper)
n = 50;
types = {'mean', 'var', 'mixture', 'tail', 'lognorm_mean', 'lognorm_var'};
for k=1:length(types)
type = types{k};
[theta_trial, polyatree, kolmo_smir, wilcoxon, LOR, h, h2] = powercurve(n, type, ...
'nsamples', nsamples, 'doplot', true, 'partition', 'empirical');
title(type);
end
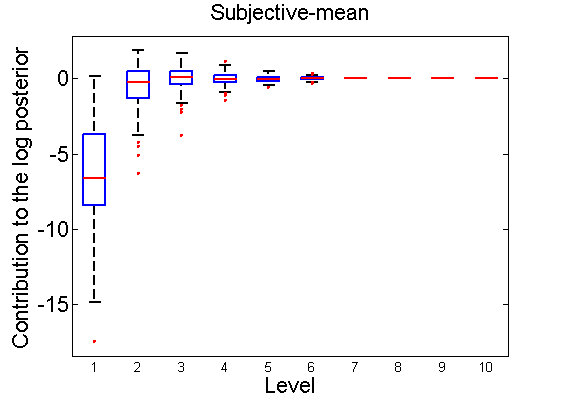
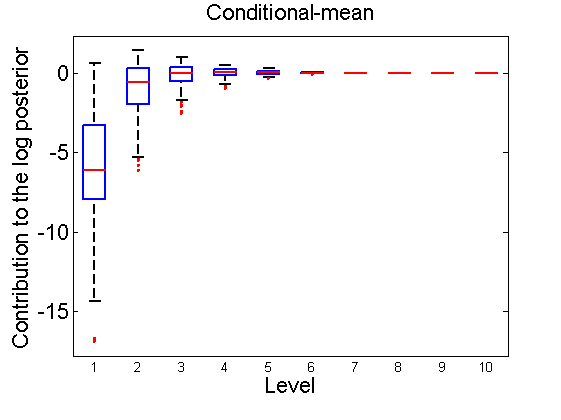
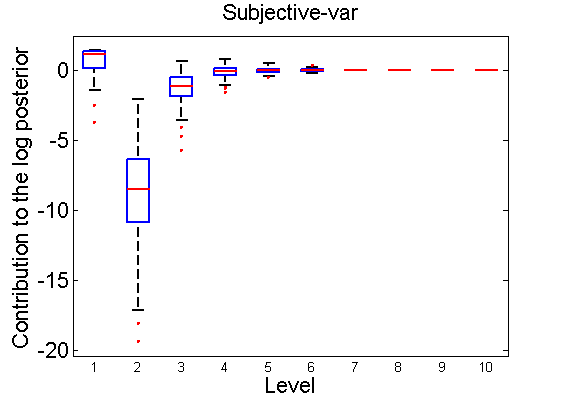
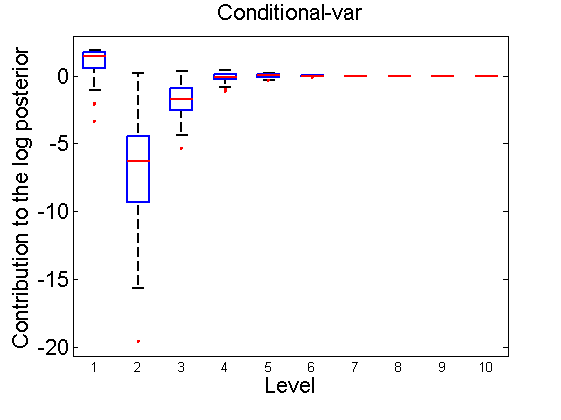
Distribution of the log-contributions at different levels of the tree
(Figure 3(a-b) and 6(a-b) in the paper)
n = 50; for i=1:nsamples % Shift in the mean y1 = randn(n, 1); y2 = 1 + randn(n, 1); [h, post, stats] = PTtest(y1, y2); LOR_Level(1:length(stats.LOR_level), i, 1) = stats.LOR_level; [h, post, stats] = PTtest(y1, y2, 'partition', 'empirical'); LOR_Level(1:length(stats.LOR_level), i, 2) = stats.LOR_level; % Shift in the variance y1 = randn(n, 1); y2 = 3 * randn(n, 1); [h, post, stats] = PTtest(y1, y2); LOR_Level(1:length(stats.LOR_level), i, 3) = stats.LOR_level; [h, post, stats] = PTtest(y1, y2, 'partition', 'empirical'); LOR_Level(1:length(stats.LOR_level), i, 4) = stats.LOR_level; end titles ={'Subjective-mean', 'Conditional-mean','Subjective-var', 'Conditional-var'}; for k=1:4 figure; if ~isoctave hb = boxplot(LOR_Level(1:10,:,k)'); set(hb, 'MarkerSize', 2, 'linewidth', 2); else hb = plot(LOR_Level(1:10,:,k), 'x'); end xlabel('Level'); ylabel('Contribution to the log posterior'); title(titles{k}) end
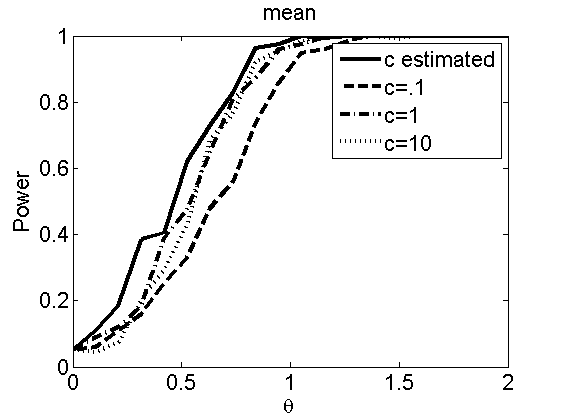
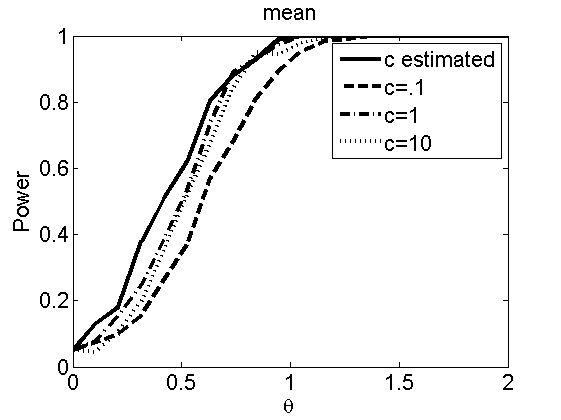
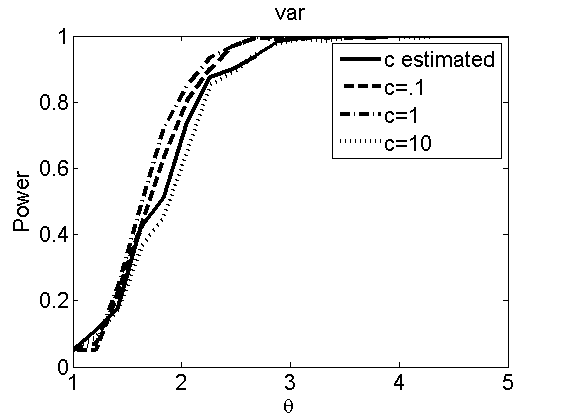
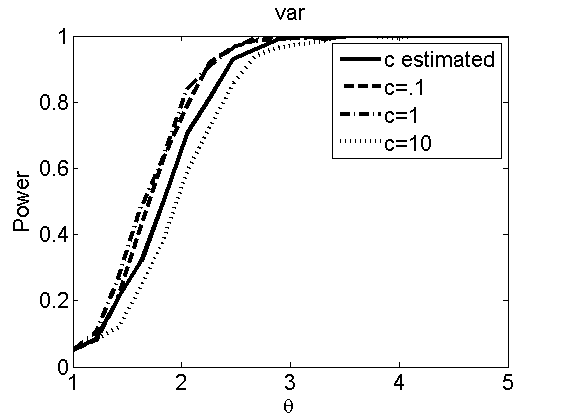
Sensibility to the parameter c
(Figures 7 and 8 in the paper)
types = {'mean', 'var'};
n = 50;
for k=1:length(types)
type = types{k};
[theta_trial, polyatree(:,1,k)] = powercurve(n, type, ...
'nsamples', nsamples, 'doplot', false, 'estimate_c', true);
[theta_trial, polyatree(:,2,k)] = powercurve(n, type, ...
'nsamples', nsamples, 'doplot', false, 'c', .1);
[theta_trial, polyatree(:,3,k)] = powercurve(n, type, ...
'nsamples', nsamples, 'doplot', false, 'c', 1);
[theta_trial, polyatree(:,4,k)] = powercurve(n, type, ...
'nsamples', nsamples, 'doplot', false, 'c', 10);
figure
plot(theta_trial,polyatree(:,:,k))
xlabel('\theta')
ylabel('Power')
legend('c estimated', 'c=.1', 'c=1', 'c=10')
title(types{k})
[theta_trial, emppolyatree(:,1,k)] = powercurve(n, type, ...
'nsamples', nsamples, 'doplot', false, 'estimate_c', true, 'partition', 'empirical');
[theta_trial, emppolyatree(:,2,k)] = powercurve(n, type, ...
'nsamples', nsamples, 'doplot', false, 'c', .1, 'partition', 'empirical');
[theta_trial, emppolyatree(:,3,k)] = powercurve(n, type, ...
'nsamples', nsamples, 'doplot', false, 'c', 1, 'partition', 'empirical');
[theta_trial, emppolyatree(:,4,k)] = powercurve(n, type, ...
'nsamples', nsamples, 'doplot', false, 'c', 10, 'partition', 'empirical');
figure
plot(theta_trial,emppolyatree(:,:,k))
xlabel('\theta')
ylabel('Power')
legend('c estimated', 'c=.1', 'c=1', 'c=10')
title(types{k})
end